顶点法线的概念及其相关计算
顶点法线的概念
平面法线是一个平面用来描述其所朝的方向的单位向量,而顶点法线则是一个顶点在某一平面上时的朝向。
这里简单描述一下顶点法线的作用:
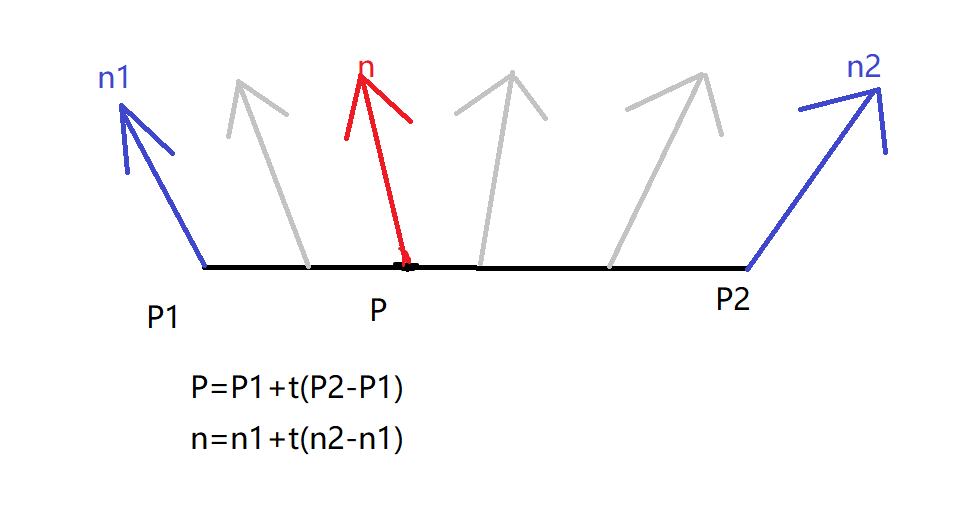
如图所示,我们通过顶点法线可以在属性插值时期计算出某个像素所对应的平面上的顶点的法线。当然,这种法线模型(如图)是不真实的,只是因为这样可以使得某些面数较少的物体也具有光滑的效果,即其面与面之间的过渡较为自然。这种方法被称为Phong差值着色。
顶点法线的计算
那么我们应如何计算顶点法线呢?我们由定义可知:顶点法线是在平面上的顶点上的,所以我们就可以由要计算的顶点所在的三角形的两条边的叉乘,求出垂直于该三角形所在平面的向量,再将之单位化,即为我们所求的顶点法线,当然,如果这个顶点同时在多个三角形上,要对各个三角形的法向量计算结果求均值。
放一段代码:
void CalculationNormalVector()
{
for(int i=0;i<m_Vertices.size();i+=3)
{
Vector3D normal=CrossProduct((m_Vertices[i+1].m_Position-m_Vertices[i].m_Position),(m_Vertices[i+2].m_Position-m_Vertices[i+1].m_Position));
m_Vertices[i].m_NormalVector=normal;
m_Vertices[i+1].m_NormalVector=normal;
m_Vertices[i+2].m_NormalVector=normal;
}
bool* flag=new bool[m_Vertices.size()];
memset(flag,false,sizeof(bool)*m_Vertices.size());
for(int i=0;i<m_Vertices.size();i++)
{
if(!flag[i])
{
vector<Vertex*> pointers;
int n=0;
Vector3D sum={0,0,0};
for(int j=i;j<m_Vertices.size();j++)
{
if(m_Vertices[i].m_Position==m_Vertices[j].m_Position)
{
n+=1;
sum=sum+m_Vertices[j].m_NormalVector;
flag[j]=true;
pointers.push_back(&m_Vertices[j]);
}
}
Vector3D ans=sum/n;
for(auto p:pointers)
{
p->m_NormalVector=ans;
}
}
}
delete[] flag;
}
法向量的转化
法向量的转化是指将某个平面改变后,如何用改变前的法向量计算出改变后的法向量。上图:
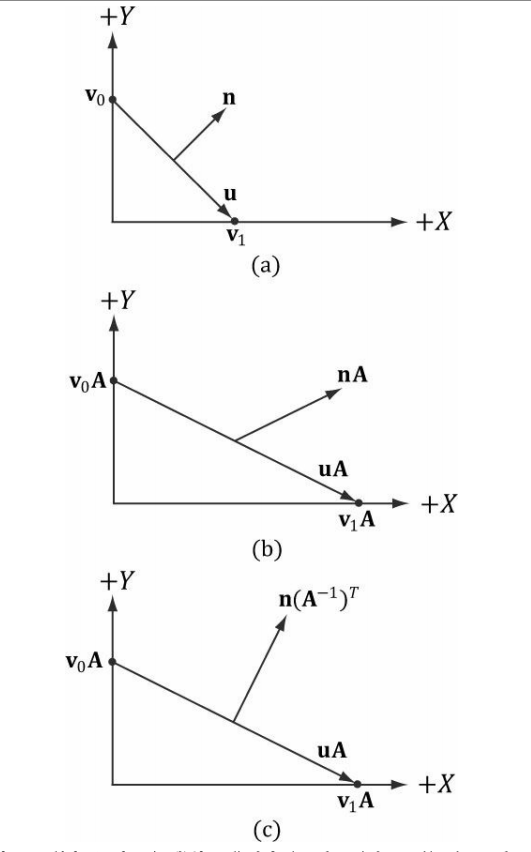
图片来自于“Introduction to 3D game programming with Direct X 11”
这里做个推导吧:
设u为平面的上任意两向量的差(也是向量)
设n是平面那个改变前的法向量。
这可知u·v=0 => 两个向量垂直
将其转化为矩阵形式:
u*T(n)=0 T(n)表示n的转置
设A为改变平面的矩阵
所以可得:u* A*I(A)*T(n)=0 I(A)表示A的逆矩阵
因为T(T(A))=A又T(A*B)=T(A)*T(B)
所以I(A)*T(n)=n*T(I(A))
所以可列出:
u*A·n*T(I(A))=0
设B=T(I(A))
则n*B即为变换后的平面的法向量了。
在实际的应用中我们往往会在Vertex Shader中使用这一矩阵(B)来计算经过世界变换后的物体的顶点上的顶点法线,这时的矩阵A即是我们物体的世界变换矩阵。
